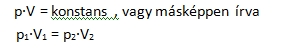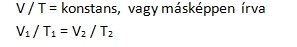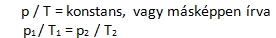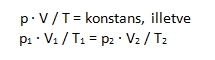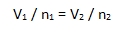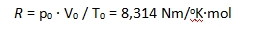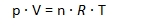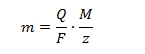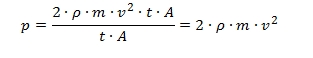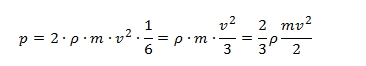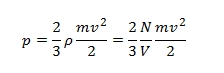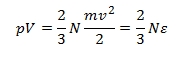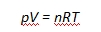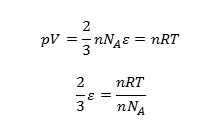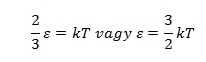| « Június 2016 » | ||||||
| H | K | Sze | Cs | P | Szo | V |
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | |||
10:43 Kémia 5 |
A kémia története 5.rész Gáztörvények A XIX. század első felében a kémikusok az új kémiai elemek felfedezése és új analitikai módszerek bevezetése mellett egyre nagyobb figyelmet fordítottak a hővel kapcsolatos folyamatok megértésére. Kialakult a hőtan, csúnyább szóval a termodinamika tudománya, melyhez a gáztörvényeken keresztül vezetett az út. A gázok kísérleti úton való tanulmányozása már jóval korábban, a XVII. században megkezdődött. Nyomásuk és térfogatuk közötti összefüggést Robert Boyle (1627-1691) ír természettudós publikálta 1662-ben. Több mint egy évtizeddel később Edme Mariotte (1620-1684) francia fizikus ugyanerre a következtetésre jutott. Mivel Boyle nem indított plágium pert, így ketten váltak a Boyle-Mariotte-törvény névadójává. Ez a törvény kimondja, hogy egy adott mennyiségű ideális gáz nyomásának és térfogatának szorzata egy adott hőmérsékleten állandó. Matematikailag kifejezve:
Némi magyarázatra szorul az ideális, vagy tökéletes gáz fogalma, mert ez az eredeti leírásban még nem szerepelt, egyszerűen gázokról volt szó. Elég körülményesen lehet meghatározni, hogy mitől ideális egy gáz, ennek talán legfrappánsabb módja azt mondani, hogy attól ideális, hogy engedelmeskedik a gáztörvényeknek. A levegő, vagy hidrogén jó közelítéssel ideális gáznak tekinthető, a propán-bután gáz már kevésbé. Ugyancsak későbbi pontosítás az adott hőmérséklet, mert a hőmérséklet hatását Boyle még nem vizsgálta. Erre jóval később Jacques Alexendre César Charles (1746-1823) francia feltaláló, matematikus és léghajós kerített sort, aki tanulmányozta a gázok térfogatának változását a hőmérséklet hatására. 1783-ban bátyjával, Roberttel együtt készítették el az első hidrogénnel töltött légballont, melynek anyaga gumival bevont selyem volt, a hidrogént vasreszelékre öntött kénsavval fejlesztették. Első alkalommal 550 m magasságig jutottak, másodszorra Charles egyedül indult és elérte a 3000 m magasságot, majd közel 400 000 néző üdvrivalgása közepette sikeresen landolt. 1787 körül 5 ballont töltött fel különböző gázokkal egyforma térfogatra, majd hőmérsékletüket 80 oC-fokra emelte. Megállapította, hogy térfogatuk egyforma mértékben növekedett. Mivel a léghajózás jobban érdekelte, eredményeit nem publikálta, helyette ezt honfitársa, Joseph Louis Gay-Lussac (1778-1850) tette meg, aki a megállapítást precíz matematikai formulába öntötte, amely így Cay-Lussac I. törvényeként maradt az utókorra. Gay-Lussac szülővárosában, Saint-Léonard-de-Noblat-ban kezdte tanulmányait, majd 1794-től Párizsban folytatta. 1802-től az Écola Polytechnique demonstrátora, 1904-től ugyanitt a kémia professzora lett. 1808-1832 között a Sorbonne fizika professzora, 1821-ben a Svéd Királyi Akadémia külső tagjává választották. Mindezek mellett lelkes léghajós volt, 1804-ben Jean Baptiste Biot francia fizikussal együtt hidrogénnel töltött léggömbjükkel 7376 m magasra emelkedtek. Megállapították, hogy a levegő hőmérséklete 174 méterenként 1 oC-kal csökken, összetétele viszont nem változik. Mérték a Föld mágneses mezőjének erősségét is, amelyben ekkora magasságig nem tapasztaltak érdemi csökkenést. Gay-Lussac egyike annak a 72 tudósnak, akinek a nevét az Eiffel torony oldalán megörökítették. Gay-Lussac I. törvénye kimondja, hogy egy állandó nyomású gáz térfogata egyenesen arányos a gáz abszolút (Kelvin fokban kifejezett) hőmérsékletével, azaz hányadosuk állandó. Képlettel:
Más megfogalmazásban: állandó nyomáson meghatározott mennyiségű gáz térfogata a 0 oC-on mért térfogatának 1 / 273,16 részével terjed ki, ha hőmérsékletét 1 oC-kal emeljük. Ennek analógiájára fogalmazódott meg Gay-Lussac II. törvénye, miszerint egy állandó térfogatú gáz nyomása egyenesen arányos a gáz abszolút hőmérsékletével, azaz hányadosuk állandó. Képlettel: Megfogalmazhatjuk úgy is, hogy állandó térfogaton meghatározott mennyiségű gáz nyomása 0 oC-on mért nyomásának 1 / 273,16 –od részével nő meg, ha hőmérsékletét 1 oC-kal növeljük. A Boyle-Mariotte és a Gay-Lussac törvények összevonásával kapjuk az egyesített gáztörvényt:
Ezzel már majdnem teljesen összeállt a kép, de néhány fontos felismerés még hátra volt. Az első Avogadro törvénye volt, miszerint a különböző gázok megegyező térfogata azonos körülmények között azonos számú részecskét tartalmaz. Másképpen fogalmazva: azonos hőmérsékleten és nyomáson a gázok térfogata anyagmennyiségükkel arányos. Ha az anyagmennyiséget mólokban fejezzük ki, írhatjuk:
Ebből az is következik, hogy bármely gáz 1 mólnyi mennyiségének térfogata azonos. Ezt a térfogatot moláris térfogatnak nevezik és standard körülmények között (normál állapot) igen pontosan megmérték. Normál állapotként 0 oC hőmérsékletet és 1 atmoszféra nyomást (1 atm = 101325 Pa) választottak, így 1 mól gáz térfogata 0,022414 m3 lett. Ezeket az értékeket visszaírva az egyesített gáztörvénybe, eredményül az univerzális gázállandót kapjuk, amely egyike a természeti törvényeket meghatározó nem túl nagyszámú állandónak.
Az R univerzális gázállandó segítségével általános összefüggés adható a gázok nyomása, térfogata, hőmérséklete, valamint mólszáma között:
Minthogy n a gáz tömegének és móltömegének hányadosa, a fenti összefüggés alkalmazható a gázok móltömegének meghatározására is. ahol M a gáz móltömege m a gáz mért tömege Már csak azt kellene tudni, hogy a moláris térfogatban lévő azonos számú részecske száma valójában mekkora, azaz hány darab atom, vagy molekula van 0,022414 m3 gáztérfogatban 0 oC hőmérsékleten és 1 atmoszféra nyomáson. Amedeo Avogadro (1766-1856) grófi származású olasz természettudós ezt a számot még nem tudta meghatározni, de később mégis az ő nevét hordozta az Avogadro-szám, vagy Avogadro-állandó. Elsőként Johann Josef Loschmidt (1821-1895) osztrák fizikus, kémikus számolta ki az állandó értékét a kinetikus gázelmélet segítségével, ezért német nyelvterületen ma is gyakran Loschmidt számnak nevezik. Mivel az értéket 1 cm3 gáztérfogatra adta meg, használata nem volt kényelmes, emiatt a moláris térfogatra vonatkozó értéke vált közismertté, amely viszont Avogadro nevéhez kötődött. Az Avogadro-szám mai értéke 6,022·1023 db/mól, később kiderült, hogy nemcsak gázokra, hanem minden anyagra érvényes. Ez az érték logikailag jóval egyszerűbb módon és sokkal pontosabban meghatározható a Faraday állandó segítségével. Michael Faraday (1791-1867) Humphry Davy tanítványaként belecsöppent az elektrolízis gyakorlatába. Kísérletező vénája miatt azonban nem elégedett meg azzal a kvalitatív képpel, hogy elektromos áram hatására egyes vegyületek pozitív és negatív töltésű ionokra disszociálnak, majd ezek a katódon, illetve anódon töltésüket elveszítve kiválnak. Tisztázni akarta az elektromos áram, és az elektródokon kiváló anyagok közötti mennyiségi összefüggéseket. Sorba kötött három elektrolizáló cellát, melyeket különböző koncentrációjú és hőmérsékletű sóoldattal töltött fel, mérte az áthaladó áram erősségét, az elektrolízis idejét és az elektródokon kivált anyagmennyiségeket. Első elektrolízis-törvényében megállapította, hogy az elektródokon kiváló anyag mennyisége arányos az áthaladó elektromos töltésmennyiséggel. (az elektromos töltésmennyiség egyenáram esetén az áramerősség és az idő szorzata Q = I·t, melyek pontosan mérhető paraméterek) Amennyiben különböző sók oldatával töltötte fel a cellákat, azt tapasztalta, hogy a kiváló anyag mennyisége arányos az anyag kémiai egyenértéksúlyával. Ezt második elektrolízis-törvénye fejezi ki. A kémiai egyenértéksúly a móltömeg és a vegyérték (oxidációs szám változás) hányadosa. Ha például az elsőbe ezüst-nitrát, a másodikba réz-szulfát, harmadikba vas-klorid oldatot öntünk, akkor az ezüst kémiai egyenértéksúlya 108 / 1 =108, a rézé 64 / 2 = 32, a vasé 56 / 3 = 18,6. Faraday azt is kimérte, hogy 1 mólnyi anyag leválasztásához mennyi elektromos töltés szükséges, ami 96 485 coulomb/mol-nak adódott. Ezt az értéket nevéről Faraday állandónak nevezték el. [Magam is megütköztem, hogy egymás mellé leírtam a kémiai egyenértéksúly és móltömeg kifejezéseket. De ez nem az én slendriánságom, hanem azon ritka esetek egyike, amikor a jó hangzás győzedelmeskedett a tudományos precizitás felett még a szaknyelvben is. Valójában kémiai egyenértéktömeget kellene írni, de ez pocsékul hangzik, maradt a súly. Korábban mólsúly volt használatos a móltömeg helyett, de ezt kiszorította a precizitás annak ellenére, hogy a móltömeg is rosszul hangzik. A tömeg és súly között azért alakult ki ez a fogalmi zavar, mert tömegről beszélünk és súlyt mérünk. Minden mérleg súlyt mér. Amikor a hentesnél 1 kilogramm marhahúst kérünk, a hentes 1 kg·9,81 m/s2 súlyú marhahúst fog kimérni, és az APEH sem avatkozik közbe, mert ténylegesen 1 kg tömegű marhahúst viszünk haza. Legalábbis bízunk benne. Fiatalabb éveimben párhuzamosan létezett a tudományos és a műszaki mértékrendszer, az elsőnek centiméter, gramm és szekundum voltak az alapegységei (CGS mértékrendszer) a másodikban a tömeg egysége, a gramm helyett az erő (súly) egysége a pond szerepelt, mondván, hogy a mérnökember azzal számol, amit mér. 1 pond = 1 gramm · g, azaz 1 gramm · 981 cm/s2, 1 kilopond = 1 kg · g, azaz 1 kg · 9,81 m/s2. A pond használatának azonban kettős baja volt az összekeverhetőség mellett. Az egyik a pontatlanság, ugyanis a nehézségi gyorsulás (g) értéke nemcsak helyről-helyre, hanem ugyanazon a mérési ponton időről-időre is változik, amit a precizitás nem tudott elviselni. Másik baja a használat kényelmében volt, mivel a g nem pontosan 10,000 m/s2, hanem 9,81…m/s2, ami megnehezítette a számolást. A Földnek legalább még egy precízen méretezett kisbolygót el kellett volna nyelnie, hogy kijöjjön a 10, de ezt nem tette meg. Persze a Természet követ el ilyen hibákat, például az 1 atmoszféra nem pontosan 1,000 bar, hanem 1,01325 bar.] Faraday két elektrolízis törvénye egy képlettel kifejezhető:
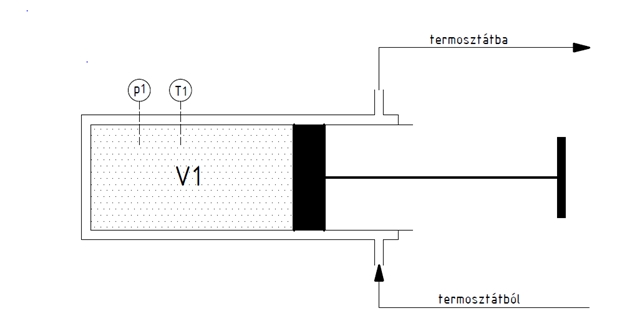
ahol: m a kivált anyag mennyisége F a Faraday állandó, 96485 C M a móltömeg z a vegyérték Amennyiben tudjuk, hogy mekkora 1 db elektronnak a töltése, azaz az elektromos elemi töltés, akkor a Faraday állandót elosztva ezzel az értékkel megkapjuk az 1 mólnyi anyagban lévő atomok, vagy molekulák számát, azaz az Avogadro számot. Az elemi töltés nagyságának közvetlen meghatározása Robert Andrews Millikan (1868-1955) amerikai fizikus nevéhez fűződik, aki kondenzátor lemezei közé beporlasztott, sztatikus elektromossággal feltöltődött olajcseppek süllyedési sebességének mérésén keresztül meghatározta azt a legkisebb közös osztót, amelynek egész számú többszörösével bármely csepp feszültsége megadható volt. Mérései szerint ez az elemi töltés 1,6·10-19 coulomb volt. Ilyen módon az Avogadro számra 96485 : 1,6·10-19 = 6,03·1023 érték adódik. A gázok állapotváltozásai jól nyomon követhetők egy termosztáthoz kapcsolódó, duplikált bicikli pumpa vázlatán. A termosztát egy hőközlő folyadékot keringető berendezés, amely alkalmas a henger belső hőmérsékletének előírt értéken való tartására, ha kell hűt, ha kell fűt.
Ha a termosztáttal a hőmérsékletet állandó értéken tartjuk és a dugattyút elmozdítjuk, akkor a henger térfogata V1-ről V2-re változik, a Boyle-Mariotte törvénynek megfelelően a nyomás p2-re nő, vagy csökken attól függően, hogy a lökethosszat csökkentettük, vagy növeltük. Amennyiben a termosztátot nem működtetjük, sőt a hengert leszigeteljük, akkor a lökethossz csökkentése a nyomás növekedése mellett hőmérsékletemelkedést is fog okozni az egyesített gáztörvény értelmében. A lökethossz növelése viszont nyomás és hőmérséklet csökkenést okoz. Ezek a törvények makroszkopikus jelenségek megfigyelésén, kísérleti méréseken alapulnak, igaz voltuk egyszerű méréssel bizonyítható. Az atomelmélet elfogadásával a fizikusokban megerősödött az a törekvés, hogy ezeknek a jelenségeknek atomi, molekuláris szintű magyarázatát keressék. A gáztörvények esetében ez Boltzmann osztrák fizikusnak sikerült a kinetikus, vagy másképpen a statisztikus gázelmélet megalkotásával. Ludwig Eduard Boltzmann (1844-1906) Bécsben született jómódú tisztviselői család gyermekeként, elemi ismereteit magántanulóként, a szülői otthonban szerezte, középiskoláit Linzben végezte. 1863-tól a Bécsi Egyetemen tanult fizikát, ahol olyan neves tanárai voltak, mint Josef Loschmidt és Joseph Stefan. Doktori disszertációját a gázok kinetikus elméletéről írta 1867-ben, a doktori fokozat megszerzése után még két évig Stefan asszisztenseként a Bécsi Egyetemen dolgozott. 1869-ben Stefan ajánlására a Grazi Egyetem matematikai fizika professzorává nevezték ki mindössze 25 éves korában. 1873-tól négy éven át a Bécsi Egyetem matematika tanára volt, majd visszatért Grazba, ahol a kísérleti fizika tanszéket vezette 14 éven keresztül. 1876-ban vette feleségül Henriette von Aigentler-t, egy tehetséges matematika-fizika tanárnőt. Házasságukból négy lány és két fiú született. 1890-től a Müncheni Egyetem elméleti fizika tanszékét vezette, majd 1893-tól korábbi tanárát, Stefant követte a Bécsi Egyetem elméleti fizika tanszékén. Boltzmann jó kapcsolatokat ápolt korának legtöbb tudósával, de jó néhányan támadták teóriáit, az ezek védelmére folytatott küzdelem felemésztette egészségét, súlyos depresszióba merült és 1906-ban egy svájci vakáció alatt felakasztotta magát. Szomorú sorsa azonban nem homályosítja el több évtizedes tudományos munkásságát, amely a század egyik kiemelkedő elméleti fizikusává emelte. A kinetikus gázelmélet a legtöbb ember számára ijesztő kifejezés, amely azt sugallja, kár a próbálkozásért úgysem fogod megérteni. Valójában a logikája nem túl bonyolult, a matematikai levezetést egyszerűsítve jól nyomon követhető. Próbáljuk meg! Tételezzük fel, hogy a gázok atomjai, vagy molekulái apró gömbök, melyek nagy sebességgel cikáznak a szélrózsa minden irányába, de elég messze vannak egymástól ahhoz, hogy egymásba ütközzenek. Most alakítsuk át jól bevált bicikli pumpánkat téglatest formára és vizsgáljuk meg egy kiválasztott részecske mozgását a dugattyú közelében. Az egyes atomok, vagy molekulák sebességét külön-külön nem ismerjük, de számolhatunk egy átlagos v sebességgel, amellyel a részecske éppen a dugattyú felé tart. Így impulzusa m·v, t idő múlva nekiütközik a dugattyúnak és onnan rugalmasan visszapattan. Sebességének nagysága ugyanaz marad, de iránya ellenkező, azaz –v lesz, impulzusa pedig m·v-ről m·(-v)-re változik, azaz az impulzus változás m·v - m·(-v) = 2m·v lesz. t idő alatt a részecske t·v utat fut be, így minden olyan részecske, amely az adott pillanatban a t·v·A képzeletbeli szelvényen belül tartózkodik, ugyancsak nekiütközik a dugattyúnak. (ahol A a dugattyú felülete) Ha egy térfogategységben ρ számú molekula van, azaz ρ = N/V, akkor a 0 és t időpont között az összes impulzusváltozás = 2·m·v·ρ·v·t·A. Mivel a sebességváltozás / idő = gyorsulás, az impulzusváltozás / idő = erő, a nyomás pedig erő / felület, azaz impulzusváltozás / idő · felület, írhatjuk:
Mivel a részecskék a téglatest mind a 6 lapja felé egyforma valószínűséggel tartanak, a dugattyúra ható nyomás az előbb számítottnak csak hatod része, azaz
Mivel ρ = N/V, írhatjuk
Ha az egyenlet mindkét oldalát megszorozzuk V-vel, ismerős képlethez jutunk:
Az egyenlet baloldalán a nyomás és térfogat szorzata áll, a jobboldalon lévő mv2/2 kifejezés pedig nem más, mint egyetlen részecske mozgási, más szóval kinetikus energiája, . Ha most felírjuk az ideális gázok állapotegyenletét:
láthatjuk, hogy a két egyenlet baloldala megegyezik, így a jobboldalaknak is egyezniük kell. Különbség, hogy az állapotegyenletben n a mólok számát, nálunk pedig N a molekulák számát jelöli. Az egyiket a másikból az Avogadro szám (1 mólban lévő molekulák száma) segítségével számíthatjuk ki, n·NA = N.
n-nel egyszerűsítve és bevezetve a k = R/NA Boltzmann állandót, írhatjuk:
Ezzel elértük célunkat. Levezettük, hogy a nyomóerőt a gázteret határoló falaknak ütköző részecskék hozzák létre, bebizonyítottuk, hogy a nyomás és térfogat szorzata a részecskék számának és átlagos kinetikus energiájának szorzatával arányos, ebből pedig arra következtettünk, hogy a részecske átlagos kinetikus energiája a hőmérséklettel áll egyszerű kapcsolatban. Persze nem értünk a kinetikus gázelmélet mélyére és végére, de ez nem is állt szándékunkban. A leglényegesebb gondolatot, miszerint a makroszkopikus jelenségeknek molekuláris szintű okai és magyarázatai vannak, és ezek visszavezethetők a mechanika alaptörvényeire, mégiscsak sikerült levezetnünk.
|
|
|
| Összes hozzászólás: 0 | |